Fibonaccispiralen
Fibonacci var en matematiker från Italien. Han skapade en egen talserie för att beskriva tillökningen hos kaniner, men talserien dyker upp överallt i naturen.
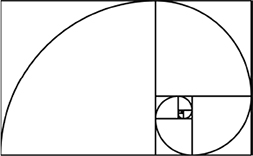
En spännande sak med Fibonaccis talserie är att den dyker upp överallt i naturen; i blommors fröställningar, på ananaser, i kålhuvuden och till och med i hela galaxer.
På kottar sitter fjällen i spiralform, både medsols och motsols. Antalet spiraler som går åt ena hållet är ett tal i fibonacciserien. Räknar vi spiralerna som går åt andra hållet upptäcker vi ett fibonaccital som är granne till det första talet.
Titta på skulpturen
Skulpturens pelare står placerade längs en fibonaccispiral och pelarnas höjd motsvarar seriens tal.
Höjden på varje stapel bestäms av höjden på de två föregående, det vill säga, varje tal i talserien är summan av de två föregående.
0+1 = 1
1+1 = 2
2+3 = 5
5+8 = 13
etc.
En av världens mest kända talserier ser ut så här: 1, 1, 2, 3, 5, 8, 13, 21, 34, …
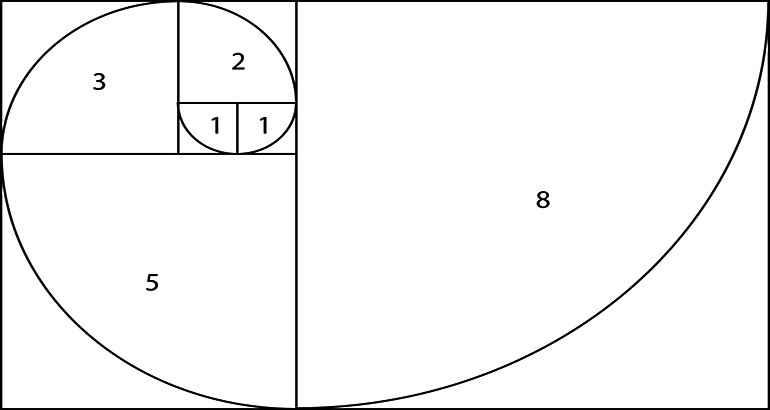
Kvadraternas sidlängder följer talserien. I varje kvadrat ritas en kvartscirkel in och därefter kan du se hur spiralen rör sig.
IN ENGLISH
Fibonacci spiral
Fibonacci was a mathematician from Italy. He created his own series of numbers to describe the birth rate of bunnies.
What is exciting about Fibonacci’s series of numbers is that it occurs everywhere in nature: in flowers, on pineapples, on cabbage heads and even in entire galaxies.
The scales on pine cones are arranged in spirals, both clockwise and counterclockwise. The number of spirals going one way is a number in Fibonacci’s series of numbers. If you count the spirals going the other way you will notice this number appearing in the spiral next to the first one.
This is how the Fibonacci spiral is constructed. The pillars follow a series of numbers. Can you see according to what pattern the height of the pillars and the series of numbers increase?
The pillars of the sculpture are placed in a Fibonacci spiral and the height of the pillars correlate to the series of numbers.
The height of each pillar is created by the two previous numbers. That is; every number in the series is created by taking the two previous numbers and adding them together.
0+1 = 1
1+1 = 2
2+3 = 5
5+8 = 13
etc.
One of the world’s most famous seriers of numbers looks like this: 1, 1, 2, 3, 5, 8, 13, 21, 34, …
The length of the sides of the squares follow the series of numbers. In each square, a quarter of a circle is drawn and you can then see the spiral moving accordingly.

