Tornet i Hanoi
Tornet i Hanoi är ett gammalt matematikproblem. Vår variant av tornet i Hanoi består av sju skivor. Uppdraget är att flytta hela tornet från en pelare till en annan.
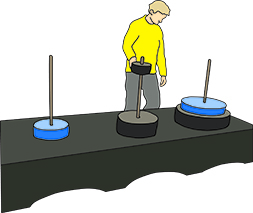
En större skiva får aldrig läggas på en som är mindre och det är bara tillåtet att flytta en skiva i taget.
Börja med tre skivor på en pelare. Hur många förflyttningar måste du göra för att få över hela tornet till en annan pelare?
Tror du att du redan funnit minsta antalet förflyttningar? Om inte, prova igen tills du kommer ner till minsta antalet. Anteckna ditt resultat.
Fortsätt på samma sätt med fyra, fem, sex och till slut sju skivor.
Titta på dina anteckningar. Kan du se något mönster i hur antalet förflyttningar ökar för varje skiva som läggs till?
Kan du beskriva mönstret?
Om du har lyckats finna minsta möjliga antal förflyttningar, och dessutom fyllt på med torn som bara består av en och två skivor, har du en rad som ser ut så här:
Antal skivor med antal förflyttningar inom parentes: 1(1), 2(3), 3(7), 4(15), 5(31), 6(63), 7(127).
Tittar vi på antalet förflyttningar ser vi att det blir dubbelt så många förflyttningar + 1 för varje ny skiva som läggs till.
IN ENGLISH
The tower of Hanoi
The tower in Hanoi is an old mathematical problem. Our variant of the tower in Hanoi consists of seven disks. The mission is to move the entire tower from one pillar to another.
A larger disc must never be placed on a smaller one and it is only allowed to move one disc at a time. Start with three slices on a pillar. How many moves do you have to make to get across the entire tower to another pillar? Do you think you have already found the minimum number of transfers? If not, try again until you reach the minimum number.
Record your result. Continue in the same way with four, five, six and finally seven discs. Look at your notes. Can you see any pattern in how the number of moves increases for each disc added?
Can you describe the pattern?
If you have managed to find the smallest possible number of movements, and also filled with towers that only consist of one and two slabs, you have a row that looks like this:
Number of discs with number of movements in parentheses: 1 (1), 2 (3), 3 (7), 4 (15), 5 (31), 6 (63), 7 (127).
If we look at the number of transfers, we see that there will be twice as many transfers + 1 for each new disc that is added.

